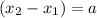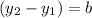Explain how the distance formula can prove Pythagoras' Theorem. In your explanation use the Pythagoras Theorem and how the distance formula can be used with a right triangl…

Question

asked Dec 17, 2023 187k views

1 Answer

John Cowan · Answer 1 · 2023-12-22T04:05:07+0000

Answer:

Given a triangle ABC, Pythagoras' Theorem shows that:

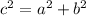
c^2=a^2+b^2

Thus,

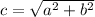
c = √(a^2+b^2)

The distance formula, gives an equivalent expression based on two points at the end of the hypotenuse for a triangle.

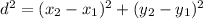
d^2 = (x_(2) -x_(1))^2 + (y_(2) -y_(1))^2

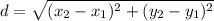
$d = \sqrt{(x_(2)-x_(1))^2 + (y_(2) -y_(1))^2 }$

Therefore when given the hypotenuse with endpoints at

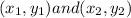
$(x_(1), y_(1)) and {(x_(2), y_(2))$

We know that the third point of the right triangle will be at

(x_(2), y_(1))

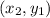
and that the two side lengths will be defined by the absolute values of:

(x_(2) - x_(1)) = a

(y_(2) - y_(1)) = b