Answer:
There are 5847.95 lines per cm for the grating.
Step-by-step explanation:
Given that,
Wavelength of mercury line,
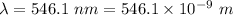
Angle in the third order spectrum,
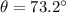
Using the grating equation, we get :
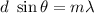
Here, m = 3
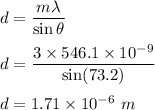
Let there are N lines for the grating. So,
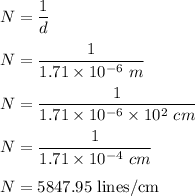
So, there are 5847.95 lines per cm for the grating.