Question

On any given day, mail gets delivered by either Alice or Bob. If Alice delivers it, which happens with probability 1/4 , she does so at a time that is uniformly distributed between 9 and 11 . If Bob delivers it, which happens with probability 3/4 , he does so at a time that is uniformly distributed between 10 and 12 . The PDF of the time X that mail gets delivered satisfies a) fX(9.5)= unanswered b) fX(10.5)=

Answer 1

(a) The value of fₓ (9.5) is 0.125.

(b) The value of fₓ (10.5) is 0.50.

Explanation:

Let X denote delivery time of the mail delivered by Alice and Y denote delivery time of the mail delivered by Bob.

It i provided that:

`X\sim U(9, 11)\\Y\sim U(10, 12)`

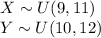
The probability that Alice delivers the mail is, p = 1/4.

The probability that Bob delivers the mail is, q = 3/4.

The probability density function of a Uniform distribution with parameters [a, b] is:

`f(x)=\left \{ {{(1)/(b-a);\ a, b>0} \atop {0;\ otherwise}} \right.`

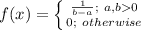
The probability density function of the delivery time of Alice is:

`f(X_(A))=\left \{ {{(1)/(b-a)=(1)/(2);\ [a, b]=[9, 11]} \atop {0;\ otherwise}} \right.`

The probability density function of the delivery time of Bob is:

`f(X_(B))=\left \{ {{(1)/(b-a)=(1)/(2);\ [a, b]=[10, 12]} \atop {0;\ otherwise}} \right.`

(a)

Compute the value of fₓ (9.5) as follows:

For delivery time 9.5, only Alice can do the delivery because Bob delivers the mail in the time interval 10 to 12.

The value of fₓ (9.5) is:

`f_(X)(9.5)=p.f(X_(A))+q.f(X_B})\\=((1)/(4)* (1)/(2))+((3)/(4)*0)\\=(1)/(8)\\=0.125`

Thus, the value of fₓ (9.5) is 0.125.

(b)

Compute the value of fₓ (10.5) as follows:

For delivery time 10.5, both Alice and Bob can do the delivery because Alice's delivery time is in the interval 9 to 11 and that of Bob's is in the time interval 10 to 12.

The value of fₓ (10.5) is:

`f_(X)(10.5)=p.f(X_(A))+q.f(X_B})\\=((1)/(4)* (1)/(2))+((3)/(4)*(1)/(2))\\=(1)/(8)+(3)/(8)\\=0.50`

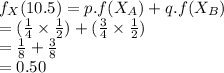
Thus, the value of fₓ (10.5) is 0.50.