Question

A box is sliding with a speed of 4.50 m/s on a horizontal surface when, at point P, it encounters a rough section. The coefficient of friction there is not constant; it starts at 0.100 at P and increases linearly with distance past P, reaching a value of 0.600 at 12.5 m past point P. (a) Use the work–energy theorem to find how far this box slides before stopping. (b) What is the coefficient of friction at the stopping point? (c) How far would the box have slid if the friction coefficient didn’t increase but instead had the constant value of 0.100?

Answer 1

The answers to the question are;

(a) The distance the box slides before stopping is 5.11 m.

(b) The coefficient of friction at the stopping point is 0.304 m

(c) The distance the box would have slid if the friction coefficient didn’t increase but instead had the constant value of 0.100 is 10.32 m

Step-by-step explanation:

Here, we note that

Initial velocity of box, v = 4.50 m/s

Final velocity of box, u = 0 m/s

Start friction of rough section μ₀ = 0.100

Max friction μ
`_{max` = 0.600

Distance of friction increase = 12.5 m

Therefore since μ varies with distance linearly, we have

The slope given by
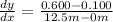`(dy)/(dx) = (0.600-0.100)/(12.5 m-0 m)` = 0.04

Therefore the equation is

f(μ) = Ax + B

and when x = 0, (The starting point) μ₀ = 0.100

Therefore B = 0.100 and A = The slope = 0.04

The equation is μ(x) = Ax + B = 0.04·x + 0.100

The work done is then found by summing the work done along the length of the rough path as follows

W =

`\int\limits^x_0 {F} \, dx = \int\limits^x_0 {-\mu}(x)mg \, dx = \int\limits^x_0 {(0.04\cdot x+0.01)\cdot mg \, dx`

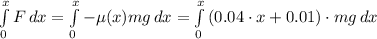
Which gives W = -m·g·(0.02·x²+0.1·x)

Equating the work done to the change i kinetic energy, we have,

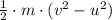`(1)/(2)\cdot m\cdot (v^(2) -u^(2) )` =-m·g·(0.02·x²+0.1·x)

From where we have

`(1)/(2)`((4.50 m/s)²- (0 m/s)²) = 9.81×0.02·x² + 0.1·x = 0.1962·x² + 0.981·x

10.125 m²/s² = 0.1962·x² + 0.981·x

That is 0.1962·x² + 0.981·x- 10.125 m²/s² = 0

Dividing both sides by 0.1962, we get

x² + 5·x - 51.61 = 0

Factorizing, we have

(x+10.11)(x-5.11) = 0

Therefore x = -10.11 m/s or x = 5.11 m

Since we are working with positive values of motion, the proper solution is

x = 5.11 m.

(b) The coefficient of friction at the stopping point is given by;

Substituting the value of x into the equation for increasing friction, we get

μ(x) = 0.04·x + 0.100 → 0.04·5.11 + 0.100 = 0.304 m

Coefficient of friction at stopping point μ(x) = 0.304 m.

(c) With a constant frictional force, we have

F = -μ·m·g

Work done = Force × Distance = -μ·m·g·x =
`(1)/(2)\cdot m\cdot (v^(2) -u^(2) )`

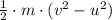
Therefore

-μ·g·x =
`(1)/(2)\cdot (v^(2) -u^(2) )`

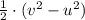
-0.1 × 9.81×x =
`(1)/(2)\cdot (0^(2) -4.5^(2) )`

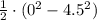
x =
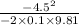`(-4.5^(2) )/(-2* 0.1*9.81)` = 10.32 m

The distance the box will slide under constant friction is 10.32 m.

Answer 2

a) xf = 5.1 m

b) u = 0.304

c) x = 10.3 m

Step-by-step explanation:

we will use the following formula:

u = 0.1 + A*x

Si x = 12.5 m, u = 0.6

Clearing A:

A = 0.5/12.5 = 0.04 m^-1

a) we have to:

W = Ekf - Eki

where Ekf = final kinetic energy

Eki = initial kinetic energy

9.8*(0.1xf + ((0.04*xf^2)/(2))) = (4.5^2)/(2)

Clearing xf, we have:

xf = 5.1 m

b) Replacing values for u:

u = 0.1 + (0.04*5.1) = 0.304

c) Wf = Ekf - Eki

-u*m*x*g = 0 - (m*v^2)/2

Clearing x:

x = v^2/(2*u*g) = (4.5^2)/(2*0.1*9.8) = 10.3 m