Question

The following three particles all have the same total energy E: (a) a photon, (b) a proton, and (c) an electron. Rank the magnitudes of the particles’ momenta from greatest to smallest.

Answer 1

The required order will be p₁ > p₂ > p ₃ .

Step-by-step explanation:

Momentum of a particle is given by :-

p =
`√(2mE)`

So, Momentum of a proton will be :-

p₂ =
`\sqrt{2m_(2) E}`

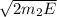
And Momentum of an electron will be :-

p₃ =
`\sqrt{2m_(3) E}`

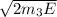
where m₂ = mass of a proton = 1.67 × 10⁻²⁷ kg

m₃ = mass of an electron = 9.1 × 10⁻³¹ kg

Also, Momentum of a photon is given by :-

p₁ =
`(E)/(c)`

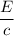
where c = speed of light in vacuum = 3 × 10⁸ m/s.

Thus, from equations (1), (2) , (3), we get

p₁ > p₂ > p ₃