Question

Calculate the pH of a buffer that is prepared by mixing 25.0 mL of 0.300 M methylamine (CH3NH2) and 0.405 g of methylammonium chloride with water to make 500.0 mL of solution.

Answer 1

Answer: The pH of the solution is 10.74

Step-by-step explanation:

• For methylammonium chloride:

To calculate the number of moles, we use the equation:

`\text{Number of moles}=\frac{\text{Given mass}}{\text{Molar mass}}`

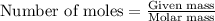
Given mass of methylammonium chloride = 0.405 g

Molar mass of methylammonium chloride = 67.52 g/mol

Putting values in above equation, we get:

`\text{Moles of methylammonium chloride}=(0.405g)/(67.52g/mol)=0.00599mol`

• For methylamine:

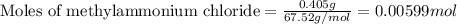
To calculate the number of moles for given molarity, we use the equation:

`\text{Molarity of the solution}=\frac{\text{Moles of solute}}{\text{Volume of solution (in L)}}`

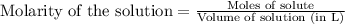
Molarity of methylamine solution = 0.300 M

Volume of solution = 25 mL = 0.025 L

Putting values in above equation, we get:

`0.300M=\frac{\text{Moles of methylamine}}{0.025L}\\\\\text{Moles of methylamine}=(0.300mol/L* 0.025L)=0.0075mol`

Total volume of the solution = [25 + 500] = 525 mL = 0.525 L (Conversion factor: 1 L = 1000 mL)

To calculate the pOH of basic buffer, we use the equation given by Henderson Hasselbalch:

`pOH=pK_b+\log(([salt])/([base]))`

`pOH=pK_b+\log(([CH_3NH_3^+Cl^-])/([CH_3NH_2]))`

We are given:

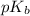`pK_b` = negative logarithm of base dissociation constant of methylamine = 3.36

`[CH_3NH_2]=(0.0075)/(0.525)`

`[CH_3NH_3^+Cl^-]=(0.00599)/(0.525)`

pOH = ?

Putting values in above equation, we get:

`pOH=3.36+\log (((0.00599/0.525))/((0.0075/0.525))\\\\pOH=3.26`

To calculate the pH of the solution, we use the equation:

`pH+pOH=14\\\\pH=14-3.26=10.74`

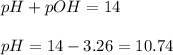
Hence, the pH of the solution is 10.74