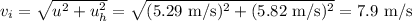Question

A 35 g steel ball is held by a ceiling-mounted electromagnet 4.0 m above the floor. A compressed-air cannon sits on the floor, 4.4 m to one side of the point directly under the ball. When a button is pressed, the ball drops and, simultaneously, the cannon fires a 25 g plastic ball. The two balls collide 1.2 m above the floor. What was the launch speed of the plastic ball?

Answer 1

7.9 m/s

Step-by-step explanation:

When both balls collide, they have spent the same time for their motions.

Motion of steel ball

This is purely under gravity. It is vertical.

Initial velocity, u = 0 m/s

Distance, s = 4.0 m - 1.2 m = 2.8 m

Acceleration, a = g

Using the equation of motion

`s = ut+(1)/(2)at^2`

`2.8 \text{ m} = 0+(gt^2)/(2)`

`t = \sqrt{(5.6)/(g)}`

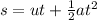
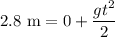
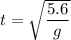
Motion of plastic ball

This has two components: a vertical and a horizontal.

The vertical motion is under gravity.

Considering the vertical motion,

Initial velocity, u = ?

Distance, s = 1.2 m

Acceleration, a = -g (It is going up)

Using the equation of motion

`s = ut+(1)/(2)at^2`

`1.2\text{ m} = ut-(1)/(2)gt^2`

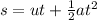
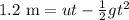
Substituting the value of t from the previous equation,

`1.2\text{ m} = u\sqrt{(5.6)/(g)}-(1)/(2)* g*(5.6)/(g)`

`u\sqrt{(5.6)/(g)} = 4.0`

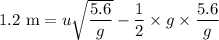
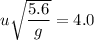
Taking g = 9.8 m/s²,

`u = (4.0)/(0.756) = 5.29 \text{ m/s}`

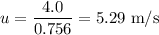
This is the vertical component of the initial velocity

Considering the horizontal motion which is not accelerated,

horizontal component of the initial velocity is horizontal distance ÷ time.

`u_h = \frac{4.4\text{ m}}{0.756\text{ s}} = 5.82\text{ m/s}`

The initial velocity is

`v_i = √(u^2+u_h^2) = \sqrt{(5.29\text{ m/s})^2+(5.82\text{ m/s})^2} = 7.9 \text{ m/s}`