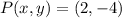Question

What are the coordinates of the point on the directed line segment from (-10, -1)(−10,−1) to (10, -6)(10,−6) that partitions the segment into a ratio of 3 to 2?

Answer 1

Therefore,

The Coordinates of the point on the directed line segment from (-10, -1) to (10,−6) that partitions the segment into a ratio of 3 to 2 is

`P(x,y)=(2,-4)`

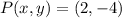
Explanation:

Given:

Let Point P ( x , y ) divides Segment AB in the ratio 3 : 2 = m : n (say)

point A( x₁ , y₁) ≡ ( -10 , -1)

point B( x₂ , y₂) ≡ ( 10 , -6)

To Find:

point P( x , y) ≡ ?

Solution:

IF a Point P divides Segment AB internally in the ratio m : n, then the Coordinates of Point P is given by Section Formula as

`x=((mx_(2) +nx_(1)) )/((m+n))\\ \\and\\\\y=((my_(2) +ny_(1)) )/((m+n))\\\\`

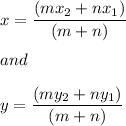
Substituting the values we get

`P(x,y)=(((3* 10 +2* -10) )/((3+2)),((3* -6 +2* -1) )/((3+2)))`

`P(x,y)=((10)/(5),(-20) )/(5))`

`P(x,y)=(2,-4)`

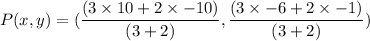
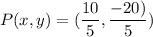
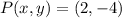
Therefore,

The Coordinates of the point on the directed line segment from (-10, -1) to (10,−6) that partitions the segment into a ratio of 3 to 2 is

`P(x,y)=(2,-4)`