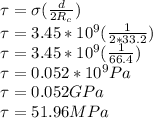Question

For some glass fiber-epoxy matrix combination, the critical fiber length-fiber diameter ratio is 33.2. Determine the fiber-matrix bond strength. Assume that the tensile strength for glass is 3.45 GPa (0.5 × 106 psi).

Answer 1

Fiber-matrix bond strength = 51.96 MPa

Step-by-step explanation:

To calculate: Fiber-matrix bond strength

Critical fiber length diameter ratio,
`(R_(c))/(d) = 33.2`

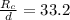
Therefore,
`(d)/(R_(c)) = (1)/(33.2)`

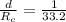
Tensile strength for glass,
`\sigma = 3.45 GPa = 3.45 * 10^(9) Pa`

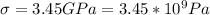
The formula for the fiber matrix bond strength is given by:

`\tau = \sigma ((d)/(2R_(c) )) \\\tau = 3.45 * 10^(9) ((1)/(2*33.2))\\ \tau = 3.45 * 10^(9) ((1)/(66.4))\\\tau = 0.052 * 10^(9) Pa\\\tau = 0.052 GPa\\\tau = 51.96 MPa`

Answer 2

The fiber-matrix bond strength is [b] 51.96MPa [/b]

Step-by-step explanation:

We are given:

`l_c = 33.2`

`Tensile strength for glass (o_f) = 3.45GPa = 3.45*10^3MPa`

We take d=1

Therefore, to find the fiber-matrix bond strength we use the formula:

`t_c = o_f * ( d / 2l_c)`;

substituting figures in the equation, we have:

`t_c = 3.45*10^3MPa * [ 1 / (2 * 33.2)]`

= 33450 * 0.015

= 51.96 MPa

Therefore the fiber-matrix bond strength is 51.96MPa