Question

The Institute of Education Sciences measures the high school dropout rate as the percentage of 16- through 24-year-olds who are not enrolled in school and have not earned a high school credential. In 2009, the high school dropout rate was 8.1%. A polling company recently took a survey of 1000 people between the ages of 16 and 24 and found 6.5% of them are high school dropouts. The polling company would like to determine whether the dropout rate has decreased. The value of the test statistic is

Answer 1

`Z_(H_0)= -1.85`

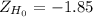
Explanation:

Hello!

The high school dropout rate, as a percentage of 16- through 24- year-olds who are not enrolled in school and have not earned a high school credential was is 2009 8.1%.

To thest the claim that this percentage has decreased, a polling company takes a random sample of 1000 people between the ages of 16 and 24 and finds out that 6.5% of them are highschool dropouts.

The study variable is

X: Number of individuals with age between 16 and 24 years old that are highschool dropouts.

The parameter of interest is the proportion fo highschool dropouts p

And the sample proportion is p'= 0.065

The hypotheses are:

H₀: p ≥ 0.081

H₁: p < 0.081

To study the population proportion, you have to approximate the distribution of the sampling proportion to normal applying the Central Limit Theorem, then the statistic to use is an approximate standard normal:

`Z_(H_0)= \frac{(p'-p)}{\sqrt{(p*(1-p))/(n) } } = \frac{0.065-0.081}{\sqrt{(0.081*0.919)/(1000) } } = -1.85`

I hope this helps!