Question

Assume I created a 95% confidence interval for the mean hours studied for a test based on a random sample of 64 students. The lower bound of this interval was 3.1416 and the upper bound was 18.6282. Assume that when I created this interval I knew the population standard deviation. Keep all decimals in your calculations. Using this information

Answer 1

(a) Width = 15.4866.

(b) Margin of error = 7.7433.

(c) Center = 10.8849.

(d) Sample mean = 10.8849.

(e) z = 1.96.

(f) Population standard deviation = 31.6053.

Explanation:

The (1 - α)% confidence interval for the population mean when the population standard deviation is known is:

`CI=\bar x\pm z_(\alpha/2){(\sigma)/(√(n))`

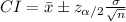
The 95% confidence interval for the mean hours studied for a test is (3.1416, 18.6282).

The sample taken was of size, n = 64.

(a)

Compute the width of the interval as follows:

`Width=Upper\ limit-Lower\ limit\\=18.6282-3.1416\\=15.4866`

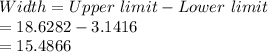
Thus, the width of the confidence interval is 15.4866.

(b)

Compute the margin of error of the interval as follows:

`MOE=(Width)/(2)=(15.4866)/(2)=7.7433`

Thus, the margin of error of the confidence interval is 7.7433.

(c)

Compute the center of the confidence interval as follows:

`Center=(Upper\ limit+Lower\ limit)/(2)=(18.6282+3.1416)/(2)=10.8849`

Thus, the center of the confidence interval is 10.8849.

(d)

The center of a (1 - α)% confidence interval is the value of the sample statistic.

In case of the confidence interval for population mean the center of the interval is the sample mean.

The value of sample mean is 10.8849.

(e)

For a 95% confidence interval the critical value of z is:

`z_(\alpha/2)=z_(0.05/2)=z_(0.025)=1.96`

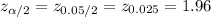
*Use a z-table for the critical value.

Thus, the value of z is 1.96.

(f)

Compute the value of standard deviation as follows:

`MOE=z_(\alpha/2)(\sigma)/(√(n))\\7.7433=1.96* (\sigma)/(√(64))\\\sigma=(7.7433* 8)/(1.96)\\\sigma=31.6053`

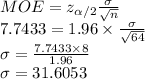
Thus, the value of population standard deviation is 31.6053.