Question

A dentist’s drill starts from rest. After 4.28 s of constant angular acceleration it turns at a rate of 28940 rev/min. Find the drill’s angular acceleration. Answer in units of rad/s 2

Answer 1

Angular acceleration, is
`708.07\ rad/s^2`

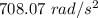
Step-by-step explanation:

Given that,

Initial speed of the drill,
`\omega_i=0`

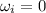
After 4.28 s of constant angular acceleration it turns at a rate of 28940 rev/min, final angular speed,
`\omega_f=28940\ rev/min=3030.58\ rad/s`

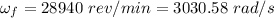
We need to find the drill’s angular acceleration. It is given by the rate of change of angular velocity.

`\alpha =(\omega_f)/(t)\\\\\alpha =(3030.58\ rad/s)/(4.28\ s)\\\\\alpha =708.07\ rad/s^2`

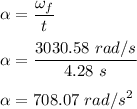
So, the drill's angular acceleration is
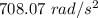`708.07\ rad/s^2`.