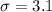Answer:
a) Mean=1.2
b) The standard deviation is
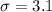
Explanation:
Given that the discrete probability distribution below :
Outcome Probability
0 0.35
1 0.36
2 0.14
3 0.08
4 0.04
5 0.02
6 0.01
a) To find the mean of this distribution :
The formula is
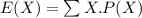
X P(X) XP(X)
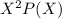
0 0.35 0 0
1 0.36 0.36 0.36
2 0.14 0.28 1.12
3 0.08 0.24 2.16
4 0.04 0.16 2.56
5 0.02 0.1 2.5
6 0.01 0.06 2.16
_________________________________________________
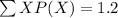
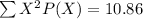
_________________________________________________
- Now substitute the value in the formula we get
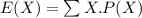
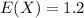
Therefore Mean=1.2
b) To find Standard Deviation :
The formula is
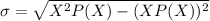
- Substitute the values i the formula we have
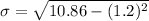
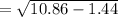
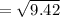
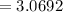
Therefore the standard deviation is