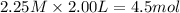Answer : The moles of
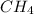 ,
,
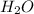 ,
,
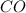 and
and
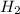 at equilibrium is, 0 mol, 1 mol, 1.5 mol and 4.5 mol respectively.
at equilibrium is, 0 mol, 1 mol, 1.5 mol and 4.5 mol respectively.
Explanation :
First we have to calculate the concentration of
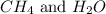

and,
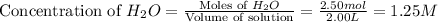
The given chemical reaction is:
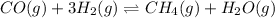
Initial conc. 0 0 0.75 1.25
At eqm. x 3x (0.75-x) (1.25-x)
The expression for equilibrium constant is:
![K_c=([CH_4][H_2O])/([CO][H_2]^3)](https://img.qammunity.org/2021/formulas/chemistry/college/uirbh6uuuuqdyelz2f8suj55l06zpn0chd.png)
Now put all the given values in this expression, we get:
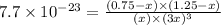
x = -2.19317 × 10¹⁰
x = 0.75
x = 1.25
x = 2.19317 × 10¹⁰
We are accepting value of x = 0.75 while all the values of x are neglecting because equilibrium concentration can not be more than initial concentration.
Equilibrium concentration of
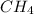 = (0.75-x) = (0.75-0.75) = 0 M
= (0.75-x) = (0.75-0.75) = 0 M
Equilibrium concentration of
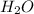 = (1.25-x) = (1.25-0.75) = 0.50 M
= (1.25-x) = (1.25-0.75) = 0.50 M
Equilibrium concentration of
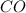 = x = 0.75 M
= x = 0.75 M
Equilibrium concentration of
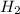 = 3x = 3(0.75) = 2.25 M
= 3x = 3(0.75) = 2.25 M
Now we have to calculate the moles of each species in terms of mole.
Moles of
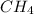 at equilibrium =
at equilibrium =
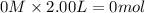
Moles of
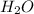 at equilibrium =
at equilibrium =
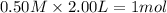
Moles of
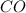 at equilibrium =
at equilibrium =
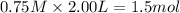
Moles of
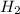 at equilibrium =
at equilibrium =