Question

3. If you were to fire a paintball pellet horizontally and at the same time drop the same type of paintball pellet you fired from the paintball gun, which pellet would hit the ground first and why is this so?

Answer 1

The paintball ball launcher

Step-by-step explanation:

The average speed of a paintball ball(vo) is approximately 90m/sec

and if the average speed of a ball pitcher in baseball (v1) is 150km/h

, which is equivalent to (150km/h*1000m/km*h/3600sec) = 41.66m/sec therefore the flight time of each mobile must be found to determine which one falls to the ground first

`Tv=(2v_(0)Sin\alpha)/(g)\\v_(01)=90(m)/(s)\\v_(02)=41.66(m)/(s)\\Tv_(0) =(2.90m/s.Sin15)/(9.8(m)/(s^(2) ) )\\Tv_(0)=(46.58m/s)/(9.8(m)/(s^(2) ) )\\Tv_(0)=4.75s\\Tv_(1) =(2.41.66m/s.Sin15)/(9.8(m)/(s^(2) ) )\\Tv_(1)=(21.56m/s)/(9.8(m)/(s^(2) ) )\\Tv_(1)=2.20s`

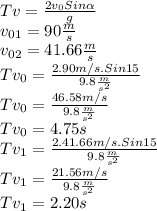
finally you can see that the shortest flight time is from the paintball ball launcher, therefore it will fall to the ground first

Note: Since the launch conditions must be the same for both, except the speed, it is placed 15º as an average value, but it can be any angle as long as it is the same for both