Answer:
Step-by-step explanation:
mass per unit length, μ = 2.33 x 10^-3 kg/m
frequency, f = 146.8 Hz
Tension, T = 82.4 N
mass per unit length of another string, μ' = 6.8 x 10^-3 kg/m
Let the tension is T'
Let the length is L.
the formula for the frequency is
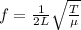
So, the frequency remains same, length remains same but the tension and the mass per unit length is different.
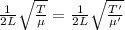
So,
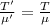
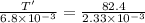
T' = 240.5 N