Question

A circular loop of flexible iron wire has an initial circumference of 165.0cm, but its circumference is decreasing at a constant rate of 12.0cm/s due to a tangential pull on the wire. The loop is in a constant, uniform magnetic field oriented perpendicular to the plane of the loop of magnitude 0.500T.

Answer 1

Step-by-step explanation:

initial circumference, C = 165 cm = 1.65 m

rate of change of circumference, dC/dt = 12 cm /s = 0.12 m/s

magnetic field, B = 0.5 T

According to the Faraday's law of electromagnetic induction

e = dФ/dt

where, Ф is the magnetic flux

Ф = B A

where, A is the area of the coil

`e=(d)/(dt)(BA)`

`e=B(dA)/(dt)`

`e=B(d(\pi r^(2)))/(dt)`

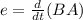
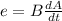
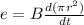
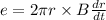`e=2\pi r* B(dr)/(dt)` ... (1)

C = 2πr

dC/dt = 2π dr/dt

Put in equation (1)

`e=C * B* (1)/(2\pi )* (dC)/(dt)`

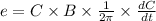
e = (1.65 x 0.5 x 0.12) / (2 x 3.14)

e = 0.016 V

Answer 2

0.005 V

Step-by-step explanation:

We are given that

Initial circumference of circular loop=C=165 cm

Rate of circumference,
`(dC)/(dt)=12 cm/s`

Magnetic field,B=0.5 T

We have to find the induced emf at time t=9 s

We know that induced amf,E=
`(Bd(A))/(dt)`

Area of circular coil,A=
`\pi r^2`

`E=B(d(\pi r^2))/(dt)=B(2\pi r)(dr)/(dt)`

Circumference of circular coil,C=
`2\pi r`

`165=2\pi r`

`r=(165)/(2\pi)`

`(dr)/(dt)=(1)/(2\pi)(dC)/(dt)=(1)/(2\pi)* (12)=(6)/(\pi) cm/s=(6* 10^(-2))/(\pi) m/s`

Radius of coil at time t=9 s

`r=(165)/(2\pi)-((6)/(\pi)* 9)=9.08 cm=9.08* 10^(-2) m`

`1 m=100 cm`

E=
`-0.5(2\pi* 9.08* 10^(-2))* (6* 10^(-2))/(\pi)=-0.005 V`

Magnitude of induced emf=0.005 V