Question

A boat is pulled into a dock by means of a rope attached to a pulley on the dock. The rope is attached to the front of the boat, which is 8 feet below the level of the pulley. If the rope is pulled through the pulley at a rate of 12 ft/min, at what rate will the boat be approaching the dock when 90 ft of rope is out?

The boat will be approaching the dock at:___________

Answer 1

The boat will be approaching the dock at 12.05 ft. per min.

Explanation:

See the attached diagram.

Let, P is the position of the pulley and B is the position of the boat.

So, from the right triangle Δ ABP,

AB² = PB² - AP² .............. (1)

= 90² - 8²

= 8036

⇒ AB = 89.64 ft.

Now, differentiating equation (1) with respect to time, t in minutes, we get

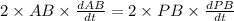`2 * AB * (dAB)/(dt) = 2 * PB * (dPB)/(dt)` {Since AP is constant}

⇒
`(dAB)/(dt) = (PB)/(AB) * (dPB)/(dt)`

⇒
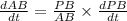
`(dAB)/(dt) = (90)/(89.64) * 12 = 12.05` ft. per minute.

Therefore, the boat will be approaching the dock at 12.05 ft. per min. (Answer)