Question

A 7.80 g bullet is initially moving at 660 m/s just before it penetrates a block of wood to a depth of 6.60 cm. (a) What is the magnitude of the average frictional force (in N) that is exerted on the bullet while it is moving through the block of wood

Answer 1

Average frictional force,f =
`2.57* 10^4\ N`

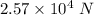
Step-by-step explanation:

Mass of the bullet,
`m_1=7.8\ g=7.8* 10^(-3)\ kg`

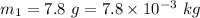
Initial speed of the bullet is 660 m/s

It penetrates a block of wood to a depth of 6.60 cm, d = 6.6 cm

It is required to find the magnitude of the average frictional force that is exerted on the bullet while it is moving through the block of wood. It is based on the concept of work energy theorem.

As it penetrates, its final speed, v = 0

`W=(1)/(2)m(v^2-u^2)\\\\-fd=-(1)/(2)mu^2`

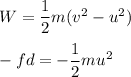
f is the frictional force

`f=(mu^2)/(2d)\\\\f=(7.8* 10^(-3)* (660)^2)/(2* 6.6* 10^(-2))\\\\f=2.57* 10^4\ N`

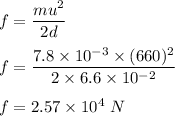
So, the average frictional force that is exerted on the bullet while it is moving through the block of wood is
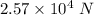`2.57* 10^4\ N`.