Answer:
The answer to the question is;
The rate at which the distance between the two cars is changing is equal to 14.4 ft/sec.
Step-by-step explanation:
We note that the distance traveled by each car after 4 seconds is
Car A = 19 ft in the west direction.
Car B = 26 ft in the north direction
The distance between the two cars is given by the length of the hypotenuse side of a right angled triangle with the north being the y coordinate and the west being the x coordinate.
Therefore, let the distance between the two cars be s
we have
s² = x² + y²
= (19 ft)² + (26 ft)² = 1037 ft²
s =
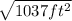 = 32.202 ft.
= 32.202 ft.
The rate of change of the distance from their location 4 seconds after they commenced their journeys is given by;
Since s² = x² + y² we have
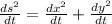
→
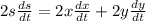 which gives
which gives
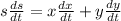
We note that the speeds of the cars were given as
Car B moving north = 12 ft/sec, which is the y direction and
Car A moving west = 8 ft/sec which is the x direction.
Therefore
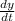 = 12 ft/sec and
= 12 ft/sec and
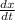 = 8 ft/sec
= 8 ft/sec
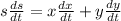 becomes
becomes
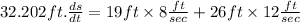 = 464 ft²/sec
= 464 ft²/sec
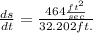 = 14.409 ft/sec ≈ 14.4 ft/sec to one place of decimal.
= 14.409 ft/sec ≈ 14.4 ft/sec to one place of decimal.