Question

What is the current in a wire of radius R = 2.02 mm if the magnitude of the current density is given by (a) Ja = J0r/R and (b) Jb = J0(1 - r/R) in which r is the radial distance and J0 = 3.74 × 104 A/m2? (c) Which function maximizes the current density near the wire’s surface?

Answer 1

Step-by-step explanation:

For this problem we have to take into account the expression

J = I/area = I/(π*r^(2))

By taking I we have

I = π*r^(2)*J

(a)

For Ja = J0r/R the current is not constant in the wire. Hence

`I(r) = \pi r^(2) J(r) = \pi r^(2) J_(0)r/R = \pi r^(3) (3.74*10^(4)A/m^(2))/(2.02*10^(-3)m)`

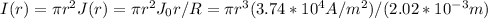
and on the surface the current is

`I(R) = \pi r^(2) J(R) = \pi r^(2) J_(0)R/R = \pi(2.02*10^(-3))^(2) (3.74*10^(4)) = 0.47 A`

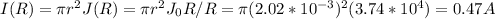
(b)

For Jb = J0(1 - r/R)

`I(r)=\pi r^(2)J(r) =\pi r^(2) J_(0)(1 - r/R)=\pi r^(2)J_(0)(1-(r)/(2.02*10^(-3)) )`

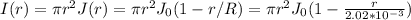
and on the surface

`I(R)=\pi r^(2)J_(0)(1-R/R)=\pi r^(2)J_(0)(1-1)= 0`

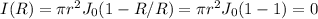
(c)

Ja maximizes the current density near the wire's surface

Additional point

The total current in the wire is obtained by integrating

`I_(T)=\pi\int\limits^R_0 {r^(2)Ja(r)} \, dr = \pi (J_(0))/(R)\int\limits^R_0 {r^(3)} \ dr =\pi (J_(0)R^(4))/(4R)=(1)/(4)\pi J_(0)R^(3)=2.42*10^(-4) A`

and in a simmilar way for Jb

`I_(T)=\pi J_(0) \int\limits^R_0 {r^(2)(1-r/R)} \, dr = \pi J_(0)[(R^(3))/(3)-(R^(2))/(2R)]=\pi J_(0)[(R^(3))/(3)-(R^(2))/(2)]`

And it is only necessary to replace J0 and R.

I hope this is useful for you

regards