Answer:
66 candies can be fitted in the pyramid shaped box.
Explanation:
If length, width and height of the rectangular box es are l, w, and h respectively.
Then volume of the rectangular box (V) = (Length × width × height)
V = lwh
Now we have to find the volume of a pyramid having length, width and height same as the rectangular box,
Then volume of the pyramid V' =
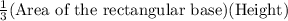
V' =
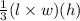
Ratio of volumes =
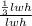 =
=

If the number of candies in the pyramid of is x then the ratio of candies in pyramid shaped box and rectangular box =
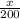
Now the ratio of volumes of the boxes will be equal to the ratio of number of candies in the boxes.
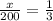
x =
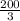
x = 66.67
x ≈ 66 candies
Therefore, 66 candies can be fitted in the pyramid shaped box.