Question

A spring of negligible mass stretches 3.00 cm from its relaxed length when a force of 7.50 N is applied. A 0.500-kg particle rests on a frictionless horizontal surface and is attached to the free end of the spring. The particle is displaced from the origin to x = 5.00 cm and released from rest at t = 0. What are the angular frequency w, the frequency, and the period of the motion?

Answer 1

ω = 22.36 Hz

f = 3.56 Hz

T = 0.28 s.

Step-by-step explanation:

a) The angular frequency (ω), can be calculated using the following equation:

`\omega = \sqrt{(k)/(m)} = \sqrt{(F)/(x*m)}`

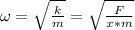
Where:

k: is the spring constant = F/x

m: is the mass of the particle = 0.500 kg

F: is the force applied = 7.50 N

x: is the displacement = 3.00 cm = 0.03 m

`\omega = \sqrt{(7.50 N)/(0.03 m*0.500 kg)} = 22.36 s^(-1) = 22.36 Hz`

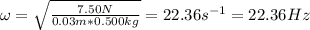
Therefore, the angular frequency of the motion is 22.36 Hz.

b) To find the frequency (f) we can use the next equation:

`f = (\omega)/(2 \pi) = (22.36 Hz)/(2 \pi) = 3.56 Hz`

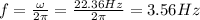
Hence, the frequency of the motion is 3.56 Hz.

c) The period (T) is equal to:

`T = (1)/(f) = (1)/(3.56 Hz) = 0.28 s`

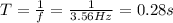
Therefore, the period of the motion is 0.28 s.

I hope it helps you!