Question

For each of the described curves, decide if the curve would be more easily given by a polar equation or a Cartesian equation. Then write an equation for the curve.

(a) A line through the origin that makes an angle of π/3 with the positive x-axis.
(b) A vertical line through the point (4, 4).

Answer 1

Answer:y = sq-rt(3) x is the equation of the curve that makes an angle π/3.

and x = 3 is the equation of line through the point (4,4)

Explanation:

Answer 2

a)
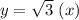`y=√(3)\ (x)` is the equation of the curve that makes an angle π/3.

b)
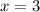`x=3` is the equation of line through the point (4,4).

Explanation:

Given:

A line from origin which makes an angle of
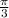`(\pi )/(3)` with x-axis.

A vertical line from
`(4,4)` .

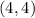We have to write the equation of the curves in Polar or Cartesian format.

Step wise:

a) A line from origin which makes an angle of
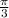`(\pi )/(3)` with x-axis.

To write the equation of the above line in Polar coordinates is more desirable as the angles could be defined well in polar form.

So,

⇒
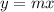`y=mx` ...equation (i)

⇒
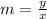`m=(y)/(x)`...here
`m` is the slope

The slope in terms of
`\theta` (angle) can be written as,

⇒
`tan(\theta)=(y)/(x)`

Plugging the values of the angle,
`\theta =(\pi )/(3)` .

⇒
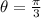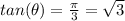`tan(\theta) =(\pi)/(3) = √(3)` ...equation (ii)

Now re-arranging the equation (i) we can write it as,

⇒
`y=√(3)\ (x)`

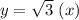
b) A vertical line from
`(4,4)` .

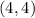Note:

The equation of a vertical line always takes the form x = k, where k is any number and k is also the x-intercept .

To write the above point in Cartesian coordinate is more acceptable and easy for us.

⇒
`x=4`

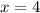
Then,

y = sq-rt(3) x is the equation of the curve that makes an angle π/3.

and x = 3 is the equation of line through the point (4,4).