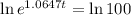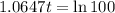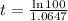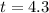Question

A bacteria culture initially contains 100 cells and grows at a rate proportional to its size. After an hour the population has increased to 290. (a) Find an expression for the number of bacteria after t hours. P(t) = (b) Find the number of bacteria after 2 hours. (Round your answer to the nearest whole number.) P(2) = bacteria (c) Find the rate of growth after 2 hours. (Round your answer to the nearest whole number.) P'(2) = bacteria per hour (d) When will the population reach 10,000? (Round your answer to one decimal place.) t = hr

Answer 1

a)
`P(t) = 100e^(1.0647t)`

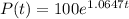
b) P(2) = 841 bacteria

c) P'(2) = 895 bacteria per hour

d) t = 4.3hr

Explanation:

The equation of growth for the number of bacteria can be modeled by the following differential equation:

`(dP)/(dt) = r`

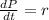
With solution.

`P(t) = P(0)e^(rt)`

In which P(t) is the population after t hours, P(0) is the initial population and r is the growth rate.

(a) Find an expression for the number of bacteria after t hours.

Initially 100 cells, so P(0) = 100.

After 1 hour, 290 cells, so P(1) = 290.

We apply this to the equation to find the value of r.

`P(t) = P(0)e^(rt)`

`290 = 100e^(r)`

`e^(r) = 2.9`

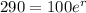
Applying ln to both sides of the equality.

`\ln{e^(r)} = ln(2.9)`

`r = 1.0647`

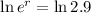
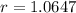
So

`P(t) = 100e^(1.0647t)`

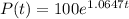
(b) Find the number of bacteria after 2 hours.

This is P(2).

`P(t) = 100e^(1.0647t)`

`P(2) = 100e^(1.0647*2)`

`P(2) = 841`

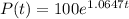
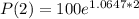
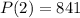
841 bacteria after 2 hours.

(c) Find the rate of growth after 2 hours.

`P(t) = 100e^(1.0647t)`

`P'(t) = 100*1.0647e^(1.0647t)`

`P'(t) = 106.47e^(1.0647t)`

`P'(2) = 106.47e^(1.0647*2)`

`P'(2) = 895`

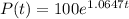
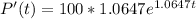
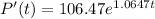
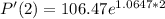
(d) When will the population reach 10,000?

This is t when P(t) = 10,000. So

`P(t) = 100e^(1.0647t)`

`10000 = 100e^(1.0647t)`

`e^(1.0647t) = (10000)/(100)`

`e^(1.0647t) = 100`

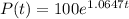
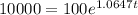
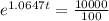
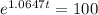
Applying ln to both sides

`\ln{e^(1.0647t)} = ln(100)`

`1.0647t = ln(100)`

`t = (ln(100))/(1.0647)`

`t = 4.3`