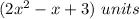Question

Todor was trying to factor 10x2 – 5x + 15. He found that the greatest common factor of these terms was 5

and made an area model:
Width
10.
-52
5
What is the width of Todor's area model?
Width =

Answer 1

The width of the area model is equal to

`(2x^2-x+3)\ units`

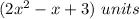
Explanation:

we know that

The area of a rectangular model is given by the formula

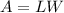`A=LW` ----> equation A

where

L is the length

W is the width

we have

`A=10x^2-5x+15`

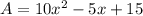
Factor the expression

`A=5(2x^2-x+3)`

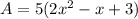
substitute the value of the Area in the equation A

`5(2x^2-x+3)=LW`

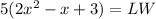
In this problem

The greatest common factor of these terms is the length (L=5 units)

so

we can say that the width is equal to (2x^2-x+3)

therefore

The width of the area model is equal to

`(2x^2-x+3)\ units`