Question

The newly elected president needs to decide the remaining 8 spots available in the cabinet he/she is appointing. If there are 14 eligible candidates for these positions (where rank matters), how many different ways can the members of the cabinet be appointed?

Answer 1

The members of the cabinet can be appointed in 121,080,960 different ways.

Explanation:

The rank is important(matters), which means that the order in which the candidates are chosen is important. That is, if we exchange the position of two candidates, it is a new outcome. So we use the permutations formula to solve this quesiton.

Permutations formula:

The number of possible permutations of x elements from a set of n elements is given by the following formula:

`P_((n,x)) = (n!)/((n-x)!)`

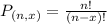
If there are 14 eligible candidates for these positions (where rank matters), how many different ways can the members of the cabinet be appointed?

Permutations of 8 from a set of 14. So

`P_((14,8)) = (14!)/((14-8)!) = 121,080,960`

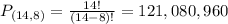
The members of the cabinet can be appointed in 121,080,960 different ways.