Question

if someone throws a ball down from a height of 100 meters, the ball's distance from the ground can be modeled by the equation: d = − 9.8 t 2 − 15 t + 100 where t is the time in seconds and d is the distance in meters. At what time (t) will the ball hit the ground? (Hint: what does this mean for d=distance?) You will get two answers. Do both make sense? (Explain in detail Why or Why not

Answer 1

The ball will hit the ground when t = 2.52s. The other answer, which is t = -4.05s, does not make sense, because the answer is an instant of time, and there are no negative time measures.

Explanation:

To solve this question, we have to find the roots of a quadratic equations, which is explained next.

Given a second order polynomial expressed by the following equation:

`ax^(2) + bx + c, a\\eq0`.

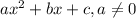This polynomial has roots
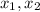`x_(1), x_(2)` such that
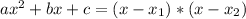`ax^(2) + bx + c = (x - x_(1))*(x - x_(2))`, given by the following formulas:

`x_(1) = (-b + √(\bigtriangleup))/(2*a)`

`x_(2) = (-b - √(\bigtriangleup))/(2*a)`

`\bigtriangleup = b^(2) - 4ac`

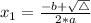
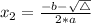
In this problem, we have that:

Ball's distance from the ground.

`d(t) = -9.8t^(2) - 15t + 100`

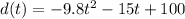
So

`a = -9.8, b = -15, c = 100`

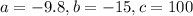
At what time (t) will the ball hit the ground?

This is t when
`d(t) = 0`. So

`\bigtriangleup = (-15)^(2) - 4*(-9.8)*100 = 4145`

`t_(1) = (-(-15) + √(4145))/(2*(-9.8)) = -4.05`

`t_(2) = (-(-15) - √(4145))/(2*(-9.8)) = 2.52`

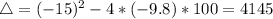
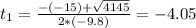
The ball will hit the ground when t = 2.52s. The other answer, which is t = -4.05s, does not make sense, because the answer is an instant of time, and there are no negative time measures.