Answer:
a) take off speed of jet in m/s = 148.3 m/s
b) we need to depress a spring for distance of 39.79 m.
Step-by-step explanation:
Given:
F = 86000 N
m =7200 kg
d = 0.92 Km= 920 m
a) To find take off speed of jet in m/s
We know that work done is given by
W = F x d ...........(equation 1)
F is force and d is displacement
Also work done in terms of kinetic energy KE and potential energy PE is given by
W = PE + KE
PE =
 m
m

Initial velocity is zero hence, PE = 0
Hence W = KE
W =
 m
m
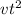 ................(equation 2)
................(equation 2)
From equation 1 and 2, we get
F x d =
 m
m
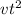
vt =
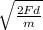
=
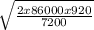
=148.25
vt = 148.3 m/s
Hence proved
b) To find how far giant spring must be depressed (in meters)
Given
spring constant K = 100000 N/m
We know that for a spring, kinetic energy KE is equal to elastic potential energy EPE
KE =
 m
m
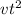
EPE =
 k
k
 , where k is spring constant and x is displacement (here distance of depression)
, where k is spring constant and x is displacement (here distance of depression)
KE = EPE
 m
m
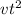 =
=
 k
k

x =
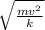
=
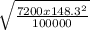
= 39.79 m
Hence we need to depress a spring of 39.79 m.