Answer:
Probability that a randomly selected woman's gestation period will be between 261 and 279 days is 0.68.
Explanation:
We are given that the average human gestation period is 270 days with a standard deviation of 9 days. The period is normally distributed.
Firstly, Let X = women's gestation period
The z score probability distribution for is given by;
Z =
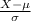 ~ N(0,1)
~ N(0,1)
where,
 = average gestation period = 270 days
= average gestation period = 270 days
 = standard deviation = 9 days
= standard deviation = 9 days
Probability that a randomly selected woman's gestation period will be between 261 and 279 days is given by = P(261 < X < 279) = P(X < 279) - P(X
 261)
261)
P(X < 279) = P(
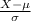 <
<
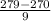 ) = P(Z < 1) = 0.84134
) = P(Z < 1) = 0.84134
P(X
 261) = P(
261) = P(
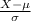

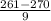 ) = P(Z
) = P(Z
 -1) = 1 - P(Z < 1)
-1) = 1 - P(Z < 1)
= 1 - 0.84134 = 0.15866
Therefore, P(261 < X < 279) = 0.84134 - 0.15866 = 0.68
Hence, probability that a randomly selected woman's gestation period will be between 261 and 279 days is 0.68.