Question

A man 6 ft tall walks at a rate of 7 ft/sec away from a lamppost that is 14 ft high. At what rate is the length of his shadow changing when he is 60 ft away from the lamppost? g

Answer 1

Let
`d` be the distance between the lamppost and the man, and
`s` the length of the man's shadow cast by light. Then the man and lamppost form a set of similar right triangles (see image) in which

`(s+d)/(14)=\frac s6`

We can solve for
`s`:

`\frac d{14}=(2s)/(21)\implies s=\frac{3d}4`

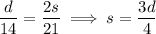
Differentiating both sides with respect to time
`t`:

`(\mathrm ds)/(\mathrm dt)=\frac34(\mathrm dd)/(\mathrm dt)`

Since
`d` is changing at a rate of 7 ft/sec, it follows that
`s` is changing at a 25% slow rate, or 7*3/4 = 21/4 = 5.25 ft/sec.