Question

A poll is given, showing 40% are in favor of a new building project. If 5 people are chosen at random, what is the probability that exactly 4 of them favor the new building project?

Answer 1

P(X = 4) = 0.077

Explanation:

We are given that a poll is given, showing 40% are in favor of a new building project. Also, 5 people are chosen at random.

The above situation can be represented through Binomial distribution;

`P(X=r) = \binom{n}{r}p^(r) (1-p)^(n-r) ; x = 0,1,2,3,.....`

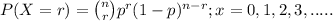
where, n = number of trials (samples) taken = 5 people

r = number of success = exactly 4

p = probability of success which in our question is % of people that

are in favor of a new building project, i.e; 40%

LET X = Number of people that are in favor

So, it means X ~
`Binom(n=5, p=0.40)`

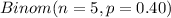
Now, Probability that exactly 4 of them favor the new building project is given by = P(X = 4)

P(X = 4) =
`\binom{5}{4}0.40^(4) (1-0.40)^(5-4)`

=
`5 * 0.40^(4) * 0.60^(1)`

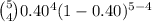
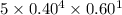
= 0.077

Therefore, Probability that exactly 4 of them favor the new building project is 0.077.

Answer 2

Answer: the probability that exactly 4 of them favor the new building project is 0.0768

Explanation:

We would assume a binomial distribution for the number of people that are in favor of a new building project. The formula is expressed as

P(x = r) = nCr × p^r × q^(n - r)

Where

x represent the number of successes.

p represents the probability of success.

q = (1 - r) represents the probability of failure.

n represents the number of trials or sample.

From the information given,

p = 40% = 40/100 = 0.4

q = 1 - p = 1 - 0.4

q = 0.6

n = 5

x = r = 4

Therefore,

P(x = 4) = 5C4 × 0.4^4 × 0.6^(5 - 4)

P(x = 4) = 5 × 0.0256 × 0.6

P(x = 4) = 0.0768