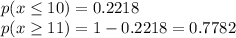Answer:
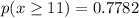
Explanation:
If a variable x follows a poisson distribution, the probability that occurs x events in a region of size t is:
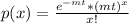
Where m is the mean per unit. So, replacing m by 7/11 because there are 7 defects per 11 square feet and t by 21 square feet, the probability that the metal sheet has x defects is:
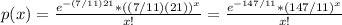
Then, the probability that a 21 square foot metal sheet has at least 11 defects is calcualted as:
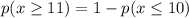
Where
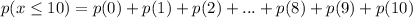
Now, p(0) is equal to:

At the same way we can calculated the other probabilities, so: