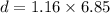Question

A large sphere rolls without slipping across a horizontal surface. the sphere has a constant translational speedof 10 m/s, a mass of 25 kg, and a radius of 0.2m. The moment of inertia of the sphere about its center of mass is I = 2/5mr^2. The sphere approaches a 25 degrees incline of height 3 m as shown and rolls up the incline without slipping. assume no energy is lost to friction. Calculate the total kinetic energy of the sphere as it rolls along the horizontal surface. Calculate the magnitude of the sphere’s velocity just as it leaves the top of the incline. Specify the direction of the sphere’s velocity just as it leaves the top of the incline. You may use any means to indicate direction accurately. Last question is neglecting air resistance, calculate the horizontal distance from the point where the sphere leaves the incline to the point where the sphere strikes the level surface.

Answer 1

Part a)

Total kinetic energy of the sphere is 1750 J

Part b)

Velocity at the top is 7.55 m/s

Part c)

horizontal distance moved by sphere is 7.95 m

Step-by-step explanation:

Part a)

As we know that the translational kinetic energy + rotational kinetic energy = Total kinetic energy

`E = (1)/(2)mv^2 + (1)/(2)I\omega^2`

`E = (1)/(2)(25)(10^2) + (1)/(2)((2)/(5)mr^2)((v^2)/(r^2))`

`E = (7)/(10)(25)(10^2)`

`E = 1750 J`

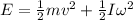
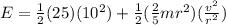
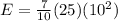
Part b)

When it reached at the top then we have

`E - mgH = (7)/(10) mv^2`

`1750 - 25(10)(3) = (7)/(10)(25)v^2`

`v = 7.55 m/s`

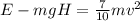
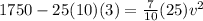
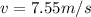
Part c)

Now we have

`v_y = 7.55 sin25 = 3.19 m/s`

`v_x = 7.55 cos25 = 6.85 m/s`

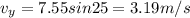
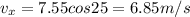
now we have

`y = v_y t + (1)/(2)at^2`

`-3 = 3.19 t - 5 t^2`

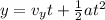
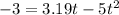
t = 1.16 s[/tex]

so the horizontal distance moved by it is given as

`d = 1.16 * 6.85`

`d = 7.95 m`