Answer:
The velocity of the steam at nozzle exit
 = 383.74
= 383.74

The volume flow rate at nozzle exit Q = 0.958
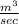
Step-by-step explanation:
Pressure at inlet
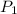 = 0.6 M pa = 600 k pa
= 0.6 M pa = 600 k pa
Velocity at inlet
 = 5
= 5

Temperature at inlet
 = 300 °c = 573 K
= 300 °c = 573 K
Temperature at outlet
 = 250 °c = 523 K
= 250 °c = 523 K
Gas constant for steam R = 0.462
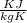
Pressure at outlet
 = 0.2 M pa = 200 k pa
= 0.2 M pa = 200 k pa
Inlet area
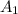 = 0.07
= 0.07

Heat loss Q = 20 KW
(a). Apply steady flow energy equation for the nozzle,
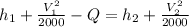
⇒ 1.8723 ( 573 - 523 ) +
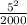 - 20 =
- 20 =
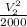
⇒
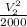 = 93.615 + 0.0125 - 20
= 93.615 + 0.0125 - 20
⇒
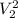 = 147255
= 147255
⇒
 = 383.74
= 383.74

This is the velocity of the steam at nozzle exit.
(b). We know that mass flow rate through the nozzle is constant at inlet and outlet and given by
m =
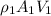 =
=
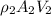 --------- ( 1 )
--------- ( 1 )

Put all the values in above equation we get,
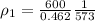
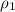 = 2.266
= 2.266
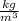
Similarly
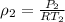
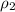 =
=
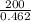 ×
×
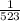
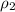 = 0.8277
= 0.8277
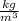
Now put all the values in equation (1),
⇒ 2.266 × 0.07 × 5 = 0.8277 ×
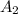 ×
×

⇒
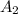 ×
×
 = 0.958
= 0.958
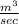
⇒ Q =
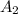 ×
×
 = 0.958
= 0.958
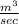
This is the volume flow rate at nozzle exit.