Question

Tutorial Exercise A boat leaves a dock at 2:00 PM and travels due south at a speed of 20 km/h. Another boat has been heading due east at 15km/h and reaches the same dock at 3:00 PM How many minutes after 2:00 PM were the two boats closest together

Answer 1

Both the boats will closet together at 2:21:36 pm.

Explanation:

Given that - At 2 pm boat 1 leaves dock and heads south and boat 2 heads east towards the dock. Assume the dock is at origin (0,0).

Speed of boat 1 is 20 km/h so the position of boat 1 at any time (0,-20t),

Formula : d=v*t

at 2 pm boat 2 was 15 km due west of the dock because it took the boat 1 hour to reach there at 15 km/h, so the position of boat 2 at that time was (-15,0)

the position of boat 2 is changing towards east, so the position of boat 2 at any time (-15+15t,0)

Formula : D=
`√((x2-x1)^2+(y2-y1)^2)`

⇒
`D = √(20^2t^2+15(t-1)^2)`

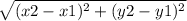
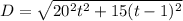
Now let
`F(t) = D^2(t)`

∵
`F'(t) = 800t + 450(t-1) = 1250t -450\\F'(t) =0`

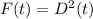
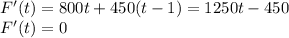
⇒ t= 450/1250

⇒ t= .36 hours

⇒ = 21 min 36 sec

Since F"(t)=0,

∴ This time gives us a minimum.

Thus, The two boats will closet together at 2:21:36 pm.