Question

Suppose a local manufacturing company claims their production line has a variance of less than 9.0. A quality control engineer decides to test this claim by sampling 35 parts. She finds that the standard deviation of the sample is 2.12. Is this enough evidence at the 1% level of significance, to accept the manufacturing companies claim?

Answer 1

`\chi^2 =(35-1)/(9) 2.12^2 =16.979`

`p_v =P(\chi^2 <16.979)=0.0065`

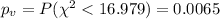
If we compare the p value and the significance level provided we see that
`p_v <\alpha` so on this case we have enough evidence in order to reject the null hypothesis at the significance level provided. And that means that the population variance is significantly lower than 9

Explanation:

Notation and previous concepts

A chi-square test is "used to test if the variance of a population is equal to a specified value. This test can be either a two-sided test or a one-sided test. The two-sided version tests against the alternative that the true variance is either less than or greater than the specified value"

`n=35` represent the sample size

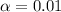`\alpha=0.01` represent the confidence level

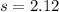`s =2.12` represent the sample deviation obtained

`\sigma_0 =3` represent the value that we want to test

Null and alternative hypothesis

On this case we want to check if the population variance specification is lower than 9 and the deviation lower than 3, so the system of hypothesis would be:

Null Hypothesis:
`\sigma^2 \geq 9`

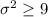
Alternative hypothesis:
`\sigma^2 <9`

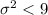
Calculate the statistic

For this test we can use the following statistic:

`\chi^2 =(n-1)/(\sigma^2_0) s^2`

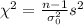
And this statistic is distributed chi square with n-1 degrees of freedom. We have eveything to replace.

`\chi^2 =(35-1)/(9) 2.12^2 =16.979`

Calculate the p value

In order to calculate the p value we need to have in count the degrees of freedom , on this case df= n-1= 35-1=34. And since is a left tailed test the p value would be given by:

`p_v =P(\chi^2 <16.979)=0.0065`

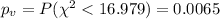
In order to find the p value we can use the following code in excel:

"=CHISQ.DIST(16.979,34,TRUE)"

Conclusion

If we compare the p value and the significance level provided we see that
`p_v <\alpha` so on this case we have enough evidence in order to reject the null hypothesis at the significance level provided. And that means that the population variance is significantly lower than 9