Answer:
![[Cl]_(eq)=(k_1[CFCl_3]_(eq))/(k_(-1)[CFCl_2]_(eq))](https://img.qammunity.org/2021/formulas/chemistry/college/7zwcu7sjhdtcawr08c77u2c8y0va3mvewc.png)
Step-by-step explanation:
Hello,
In this case, considering and rewriting the given chemical reaction, one has:

Thus, the rate equation is written as:
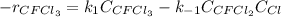
In such a way, for the equilibrium condition, the rate remains constant, that is equal to zero, hence:
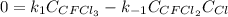
Solving for the concentration of Cl, one finally obtains:
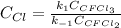
Or:
![[Cl]_(eq)=(k_1[CFCl_3]_(eq))/(k_(-1)[CFCl_2]_(eq))](https://img.qammunity.org/2021/formulas/chemistry/college/7zwcu7sjhdtcawr08c77u2c8y0va3mvewc.png)
Best regards.