Question

A sphere has a radius of 11 feet. A second sphere has a radius of 8 feet. what is the difference of the volume of thespheres

Answer 1

The difference between the volume of the spheres is 3428.88 cubic feet

Step-by-step explanation:

Given that one sphere has a radius of 11 feet.

A second sphere has a radius of 8 feet.

Volume of the 1st sphere:

The formula to determine the volume of the sphere is given by

`V=(4)/(3) \pi r^3`

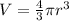
Volume of the 1st sphere is given by

`V=(4)/(3)(3.14)(11)^3`

`V=(4)/(3)(3.14)(1331)`

`V=(16717.36)/(3)`

`V=5572.45`

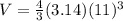
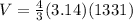
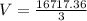
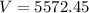
The volume of the 1st sphere is 5572.45 cubic feet.

Volume of the 2nd sphere:

Volume of the 2nd sphere is given by

`V=(4)/(3)(3.14)(8)^3`

`V=(4)/(3)(3.14)(512)`

`V=(6430.72)/(3)`

`V=2143.57`

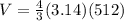
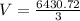
The volume of the 2nd sphere is 2143.57 cubic feet.

Difference between the volume of the two spheres:

Difference = Volume of the 1st sphere - Volume of the 2nd sphere

= 5572.45 - 2143.57

Difference = 3428.88 cubic feet.

Hence, the difference between the volume of the spheres is 3428.88 cubic feet.