Answer:
90% confidence interval for the population mean is [92.18 , 107.82].
Explanation:
We are given that as part of your study, you randomly select 30 repair costs and find the mean to be $100.00. The standard deviation of the sample is $25.20.
So, the pivotal quantity for 90% confidence interval for the population mean is given by;
P.Q. =
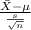 ~
~
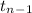
where,
 = sample mean = $100
= sample mean = $100
s = sample standard deviation = $25.20
n = sample size = 30
 = population mean
= population mean
So, 90% confidence interval for the population mean,
 is ;
is ;
P(-1.699 <
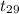 < 1.699) = 0.90
< 1.699) = 0.90
P(-1.699 <
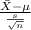 < 1.699) = 0.90
< 1.699) = 0.90
P(
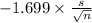 <
<
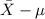 <
<
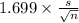 ) = 0.90
) = 0.90
P(
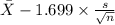 <
<
 <
<
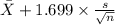 ) = 0.90
) = 0.90
90% confidence interval for
 = [
= [
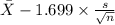 ,
,
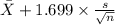 ]
]
= [
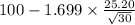 ,
,
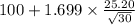 ]
]
= [92.18 , 107.82]
Therefore, 90% confidence interval for the population mean is [92.18 , 107.82].