Question

Consider the following problem: A rectangular lot whose perimeter is 1600 feet is fenced along three sides. An expensive fencing along the lot's length costs $20 per foot. An inexpensive fencing along the two side widths costs only $5 per foot. The total cost of the fencing along the three sides comes to $13,000. What are the lot's dimensions

Answer 1

The dimensions of rectangular lot is Length=500 feet and Width=300 feet

Explanation:

The formula for perimeter of rectangle is given by,

`P=2L+2W`

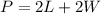
Where, L = length, W = width and P = Perimeter.

According to given data, rectangular lot has a perimeter of 1600 feet. Therefore,

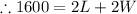`\therefore 1600=2L+2W` ….1

Now, cost of fencing along one length is given as $ 20 per feet. So total cost of one length is,

`L* \$\:20=\$\:20\:L`

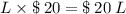
Similarly, cost of fencing along two width is given as $ 5 per feet. So total cost of two width is,

`2\:W * \$\:5=\$\:10\:W`

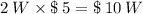
Total cost of fencing along three sides is given as $13000. Therefore,

Total cost = Cost of fencing of one length + Cost of fencing of two width

Substituting the value,

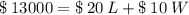`\$\:13000 = \$\:20\:L + \$\:10\:W` ….2

So, there is two equations and two unknown. Solve it by substitution method.

Solving equation 1 for W.

Dividing both sides of equation by 2,

`\therefore L+W=800`

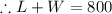
Subtracting L from both sides,

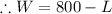`\therefore W=800-L` ….3

Substituting equation 3 into equation 1 and simplifying,

`13000=20L+10\left ( 800-L \right )`

`13000=20L+\left ( 8000-10L \right )`

`13000=10L+8000`

`13000-8000=10L`

`5000=10L`

`500=L`

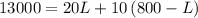
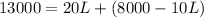
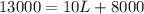
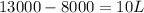
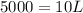
So value of length is 500 feet. Substituting the value of L in equation 1 and simplifying,

`2L+2W=1600`

`2\left ( 500 \right )+2W=1600`

`1000+2W=1600`

`2W=1600-1000`

`2W=600`

`W=300`

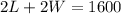
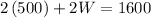
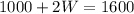
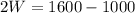
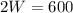
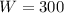
So value of width is 300 feet.