Question

In a simple linear regression problem, if the correlation coefficient is 0.98, this means that about 96% of the total variation in y can be explained by the regression line. about 98% of the x values are equal. about 96% of the y values are positive. about 96% of the total variation in x can be explained by the regression line. about 98% of the total variation in y can be explained by the regression line.

Answer 1

The % of variation is given by the determination coefficient given by
`r^2` and on this case
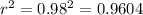`r^2 =0.98^2 =0.9604`, so then the % of variation explained by the model is 96.04%.

And the best answer would be:

About 96% of the total variation in y can be explained by the regression line

Explanation:

Previous concepts

The correlation coefficient is a "statistical measure that calculates the strength of the relationship between the relative movements of two variables". It's denoted by r and its always between -1 and 1.

And in order to calculate the correlation coefficient we can use this formula:

`r=(n(\sum xy)-(\sum x)(\sum y))/(√([n\sum x^2 -(\sum x)^2][n\sum y^2 -(\sum y)^2]))`

Solution to the problem

The % of variation is given by the determination coefficient given by
`r^2` and on this case
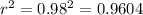`r^2 =0.98^2 =0.9604`, so then the % of variation explained by the model is 96.04%.

And the best answer would be:

About 96% of the total variation in y can be explained by the regression line