Question

Evaluate 10 m + n 2 4 10m+ 4 n 2 ​ 10, m, plus, start fraction, n, squared, divided by, 4, end fraction when m = 5 m=5m, equals, 5 and n = 4 n=4n, equals, 4.

Answer 1

`\therefore10m+\frac{n^2}4 =54`

Explanation:

Variables : The value of a quantity which can be changed.

Monomial : Monomial contains only one term.

Example 3x, 4,6y² etc.

Binomial: Binomial contains two terms.

Example 3+4y, 20+7z etc

Trinomial: Trinomial contains 3 terms.

Example 5x-2y+5, 7z-3y+4x etc.

Given that,

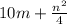`10m+\frac{n^2}4` [ It is a binomial.]

Putting m =5 and n=4

`= (10* 5)+\frac{4^2}4`

`=50+(4*4)/(4)`

`=50+4`

=54

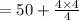
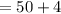
`\therefore10m+\frac{n^2}4 =54`