Question

A stone is dropped from the roof of a building. 2.00 s after that, a second stone is thrown straight down with an initial speed of 30.0 m/s. It is observed that the two stones land at the same time. a) How long did it take the first stone to reach the ground

Answer 1

So the time it takes the first stone to fall from the top of the cliff is 3.88 seconds.

Step-by-step explanation:

We can use free fall equations to describe the motion of both stones given by

`y = y_0 +v_0t- \cfrac12 gt^2`

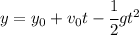
Once we have set both systems we can then solve for the time of the first stone.

Setting up free fall equations.

For the first stone, we do not know about the its initial height, nor its time, but we know it is being falling from rest so its initial velocity is 0, thus the equation that describes it will be:

`y = y_0 -\cfrac 12 gt^2`

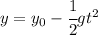
Now at the bottom or ground level we will have y = 0, thus we will have

`0= y_0 -\cfrac 12 gt^2`

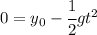
For the second stone, we know its take is 3.9 seconds past the initial time of the first stone so we will have
`t_2+2 =t`

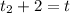
which means
`t_2 =t-2`

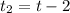
It has also an initial speed, but aiming downwards so
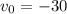`v_0= -30`. Using the given information we can write

`y = y_0 -30(t-2)- \cfrac12 g(t-2)^2`

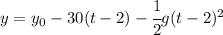
At the bottom or ground level we have y = 0

`0 = y_0 -30(t-2)- \cfrac12 g(t-2)^2`

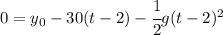
Thus we get a system of 2 equations and 2 unknowns that are the initial height
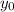`y_0` and the initial time t.

`0= y_0 -\cfrac 12 gt^20 = y_0 -30(t-2)- \cfrac12 g(t-2)^2`

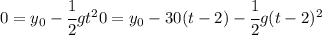
Solving the system of equations

We can solve for the height of the cliff from the first equation and plug it on the second equation.

`.0= y_0 -\cfrac 12 gt^2\\y_0 =\cfrac 12 gt^2`

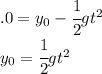
Replacing on the second equation we get

`0 = y_0 -30(t-2)- \cfrac12 g(t-2)^2\\0 =\cfrac 12 gt^2 -30(t-2)- \cfrac12 g(t-2)^2`

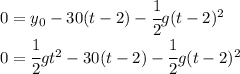
At this point we can plug the value of the gravity
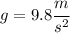`g= 9.8 \cfrac{m}{s^2}` and expand it in order to simplify it.

`0 =\cfrac 12 (9.8)t^2 -30(t-2)- \cfrac12 (9.8)(t-2)^2\\0 =4.9t^2 -30t+60- 4.9(t^2-4t+4)\\0 =4.9t^2 -30t+60- 4.9t^2+19.6t-19.6`

Combining like terms we get

`0 = -10.4t+40.4\\10t = 40.4\\t = (40.4)/(10.4) \\= 3.88`

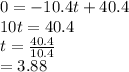
t = 3.88s

So the time it takes the first stone to fall from the top of the cliff is 3.88 seconds.