Answer:
The speed at which the water leaves the hole
 = 4.21
= 4.21

The value of diameter of the hole d = 0.112 m = 11.2 cm
Explanation:
Given data
Flow rate = 2.5 ×

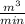 = 0.0416 ×
= 0.0416 ×

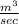
Height (h) = 16 m
(a) The speed at which the water leaves the hole :-
Apply bernouli equation for the water tank at point 1 & 2
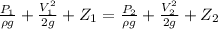 ------ (1)
------ (1)
Since
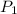 =
=
 ,
,
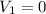 &
&
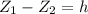
Equation (1) becomes
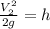
 =
=
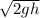
This is the speed at which the water leaves the hole.
Put the values of g & h in the above formula
⇒ 2 g h = 2 × 9.81 × 16 = 17.71
 =
=
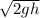 =
=
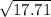
 = 4.21
= 4.21

This is the speed at which the water leaves the hole.
(b)Diameter of the hole :-
We know that flow rate Q = A × V
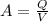
Put the values of Q & V in the above formula we get
A =
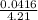 ×
×

A = 9.88 ×
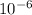
We know that area A =
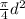
⇒
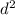 =
=
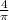 × 9.88 ×
× 9.88 ×
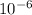
⇒
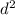 = 0.01258
= 0.01258
⇒ d = 0.112 m = 11.2 cm
this is the value of diameter of the hole.