Question

4.) The time X (minutes) for a lab assistant to prepare the equipment for a certain experiment is believed to have a uniform distribution with A = 20 and B = 50. What is the probability that preparation is within 2 minutes of the mean time?

Answer 1

`P(35-2 < X 35+2) = P(33< X< 37)= P(X<37) -P(X<32)`

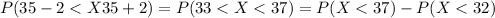
And using the cumulative distribution function we got:

`P(35-2 < X 35+2) = P(33< X< 37)= P(X<37) -P(X<32) = (37-20)/(50-20) -(33-20)/(50-20) =0.567-0.433=0.134`

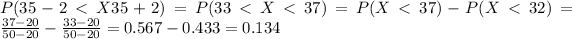
The probability that preparation is within 2 minutes of the mean time is 0.134

Explanation:

For this case we define the following random variable X= (minutes) for a lab assistant to prepare the equipment for a certain experiment , and the distribution for X is given by:

`X \sim Unif (a= 20, b =50)`

The cumulative distribution function is given by:

`F(x) = (x-a)/(b-a) , a \leq X \leq b`

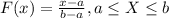
The expected value is given by:

`E(X) = (a+b)/(2) = (20+50)/(2)=35`

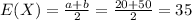
And we want to find the following probability:

`P(35-2 < X 35+2) = P(33< X< 37)`

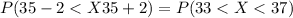
And we can find this probability on this way:

`P(35-2 < X 35+2) = P(33< X< 37)= P(X<37) -P(X<32)`

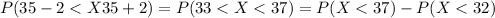
And using the cumulative distribution function we got:

`P(35-2 < X 35+2) = P(33< X< 37)= P(X<37) -P(X<32) = (37-20)/(50-20) -(33-20)/(50-20) =0.567-0.433=0.134`

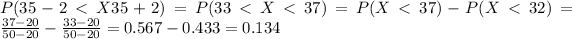
The probability that preparation is within 2 minutes of the mean time is 0.134