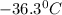Question

At what temperature (in °C) would one liter of phosphine gas, PH3, have a mass of 1.725 g, if the gas pressure is 0.9910 atm? Assume that the gas behaves ideally.

Answer 1

Answer: Temperature of one liter of phosphine gas with a mass of 1.725 g and gas pressure of 0.9910 atm is
`-36^0C`

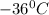
Step-by-step explanation:

According to the ideal gas equation:

PV=nRT

P = Pressure of the gas = 0.9910 atm

V= Volume of the gas= 1.0 L

T= Temperature of the gas in kelvin = ?

R= Gas constant =
`0.0821Latm/Kmol`

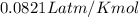
n= moles of gas=
`\frac{\text {given mass}}{\text {molar mass}}=(1.725g)/(34g/mol)=0.051ol`

`0.9910atm* 1.0=0.051* 0.0821* T`

`T=236.7K=(236.7-273)^0C=-36.3^0C`

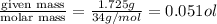
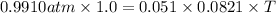
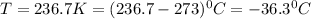
Thus the temperature (in °C) of one liter of phosphine gas with a mass of 1.725 g and gas pressure of 0.9910 atm is
`-36.3^0C`