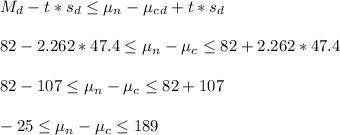Question

A maintenance manager must test a new repair method that should increase the expected time between repairs. For each machine used in the study, she recorded the last time between failures prior to using the new method, which she called, "Current", and the first time between failures after using the new method, which she called "New". These are the times (in hours):

Machine 1 2 3 4 5 6 7 8 9 10
Current 155 222 346 287 115 389 183 451 140 252
New 211 345 419 274 244 420 319 505 396 222
A) Conduct the most appropriate hypothesis test using a 0.05 significance level. Use the rejection region approach. (You must clearly specify 5 steps for your test.)
B) Calculate the p-value for the test in A
C) Construct a 95% two-sided confidence interval for the true mean difference.

Answer 1

a) The value t=1.73 < 1.833 fall in the acceptance region, so the effect is not significant. The null hypothesis can not be rejected.

The claim that the new method is better doesn't have enough statistical evidence.

b) P-value=0.06

c) 95% CI

`-25 \leq\mu_n-\mu_c\leq 189`

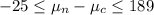
Explanation:

A) We have to test the hypothesis about the difference of the means.

The claim is that the new method gives larger times between repairs.

1) State the null and alternative hypothesis

`H_0: \mu_n\leq\mu_c\\\\H_a: \mu_n>\mu_c`

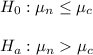
The significance level is 0.05.

2) The sample mean and standard deviation of the current method is

`M_c=254\\\\ s_c=113`

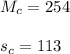
The sample mean and standard deviation of the new method is

`M_n=336\\\\ s_n=99`

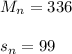
The difference of means is

`M_d=M_n-M_c=336-254=82`

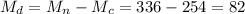
The standard deviation of the difference of means can be estimated as:

`s_d=\sqrt{(s_n^2+s_c^2)/(n) }=\sqrt{(99^2+113^2)/(10) }=√(2246)=47.4`

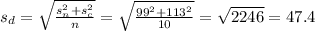
3) Then, we can calculate the t-statistic as:

`t=(M_d-(\mu_n- \mu_c))/(s_d) =(82-0)/(47.4)=1.73`

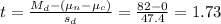
4) For 9 degrees of freedom and a significance level of 0.05, the critical value for t is t=1.833.

5) The value t=1.73 < 1.833 fall in the acceptance region, so the effect is not significant. The null hypothesis can not be rejected.

The claim that the new method is better doesn't have enough statistical evidence.

B) For a df=10-1=9 and t=1.73, the P-value is

`P(t_9>1.73)=0.06`

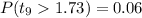
C) In this case, for 9 degrees of freedom and 95% CI, the critical value of t is t=2.262.

The CI can be written as:

`M_d-t*s_d\leq\mu_n-\mu_c\leqM_d+t*s_d\\\\82-2.262*47.4\leq\mu_n-\mu_c\leq 82+2.262*47.4\\\\82-107\leq\mu_n-\mu_c\leq 82+107\\\\-25 \leq\mu_n-\mu_c\leq 189`