Question

A piece of wire 40 cm long is to be cut into two pieces. One piece will be bent to form a circle and; the other will be bent to form a square. Find the lengths of the two pieces that cause the sum of the area of the circle and the area of the square to be a minimum. The perimeter of the square is cm The circumference of the circle is cm

Answer 1

The perimeter of circle = 17.6 cm

Perimeter of square = 22.4 cm

Explanation:

The total length of the wire = 40 cm

Let us assume the circumference of the circle = k cm

So, the circumference of the square = ( 40 - k) cm

Now,as circumference of circle = 2πR

⇒2πR = k cm or, R =
`((k)/(2\pi))`

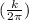
Area of the circle = πR²

or, A =
`\pi ((k)/(2\pi) )^2`

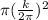
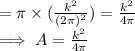`= \pi * ((k^2)/((2\pi)^2) ) = (k^2)/(4 \pi) \\\implies A = (k^2)/(4 \pi)` ....... (1)

Similarly , perimeter of square = 4 x Side

⇒ 4 x Side = ( 40 - k) cm ⇒ S =
`((40 - k)/(4) )`

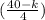
Area of the square = (Side)² =
`((40 - k)/(4) ) ^2`

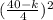
Solving, we get:
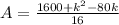`A = (1600 + k^2 - 80 k)/(16)` ....... (1)

So, combining (1) and (2), total area A is

`A = ((k^2)/(4 \pi) ) + (k^2 + 1600 - 80 k )/(16)`

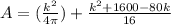
or, we get: A = 0.07962 k² + 0.0625 k² + 100 - 5 k

A = 0.1422 k² - 5 k + 100

For axis of symmetry :
`k = ((-b)/(2a) ) = (-(-5)/(2(0.1420)) = 17.6`

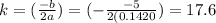
⇒ k = 17.6 inches

So, the perimeter of circle = 17.6 cm

Perimeter of square = (40 - 17.6 ) = 22.4 cm