Question

A hockey puck is sliding across a frozen pond with an initial speed of 9.5 m/s. It comes to rest after sliding a distance of 37.4 m. What is the coefficient of kinetic friction between the puck and the ice

Answer 1

The coefficient of kinetic friction between the puck and the ice is
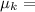`\mu _(k) =` 0.12

Step-by-step explanation:

Given :

Initial speed
`v_(o) = 9.5 (m)/(s)`

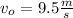
Displacement
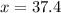`x = 37.4` m

From the kinematics equation,

`v^(2) - v^(2) _(o) = 2ax`

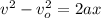
Where
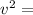`v^(2) =` final velocity, in our example it is zero (
`v =0`),
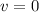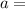`a =` acceleration.

`a =- (90.25)/( 2 * 37.4)`

`a =- 1.21 (m)/(s^(2) )`

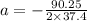
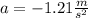
From the formula of friction,

`F =- \mu _(k ) N`

Minus sign represent friction is oppose the motion

Where
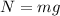`N = mg` ( normal reaction force )

`ma = -\mu _(k) m g` ( ∵
`g = 9.8 (m)/(s^(2) )` )

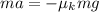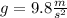So coefficient of friction,

`\mu_(k) = (1.21)/(9.8)`

`\mu_(k) = 0.12`

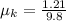
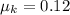
Therefore, the coefficient of kinetic friction between the puck and the ice is
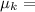`\mu _(k) =` 0.12 .